Article: Looking beyond testing for differences when conducting a Method or Technology Transfer

A question we often get asked is “Why have we failed a technology transfer when the precision of our lab’s method is excellent?” Often the answer to this question is that a traditional ‘zero-difference’ hypothesis test, such as the Student’s t-test, has been employed when in fact the goal is to demonstrate that the originating and receiving sites are in fact equivalent rather than different.

Imagine that a well-developed and controlled protein assay results in small variation or imprecision at each site. This imprecision is typically measured by a coefficient of variation, or relative standard deviation. Also, imagine that there is no practical inter-site difference between the average absorbance results, but relative to the small intra-site variation, a statistically significant t-test might incorrectly lead to a false-negative decision with the analyst concluding that the two sites are not equivalent.

Don’t just take our word for it: “Concluding equivalence or non-inferiority based on observing non-significant test result of the null hypothesis that there is no difference … is inappropriate” states ICH, whilst a BMJ article emphasises “Absence of evidence” (of a difference between sites) “is not evidence of absence” (of a difference between sites). 

The opposite can of course also be true and can lead to a false-positive but similarly incorrect decision being made. The broad imprecision of a bioassay, for example, can result in a non-statistically significant t-test, even though there is a large practical bias between the two site averages.

If the objective of a method or technology transfer is to provide evidence of equivalence, rather than evidence of a difference, Lung et. al. [1] suggest that “a more appropriate statistical question is to ask…is there an unacceptable difference between two sets of results?” Instead of testing a zero-difference null hypothesis (i.e., there is no bias between the means), Lung et. al. recommend testing the more appropriate null hypothesis: there is a bias between the means larger than that which is considered a practically “acceptable difference”.

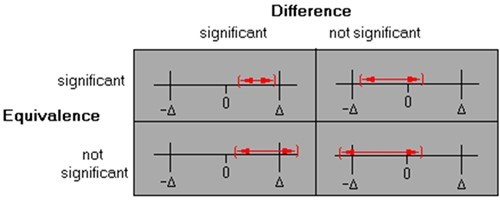
In addition to setting acceptance criteria for the precision of the method at the receiving site, this equivalence approach requires you to also define an acceptable bias (Δ) or equivalence margin, within which the inter-site difference in mean values would be judged practically and statistically significantly equivalent. Statistical tests of equivalence are commonly based on a 90% confidence interval for the difference between the site means and inferring equivalence if entire interval falls within the equivalence margin (±Δ).The conclusions for each scenario in Figure 1 might be: top left – statistically different but equivalent due to good precision; top right – not statistically different and also equivalent; bottom left – statistically different and not equivalent; bottom right – not statistically different but not equivalent due to poor precision.

Bioequivalence or equivalence statistical techniques such as the Two-One-Sided Test (TOST) and interval hypothesis testing are well established and provide a more appropriate means of analysing method transfer data superior to the traditional ‘zero-difference’ hypothesis tests for these very reasons. They overcome the problem traditional difference tests have of either -

• detecting statistically significant differences between the originating and receiving sites, perhaps because of low variability (good precision) in the method, but which are in fact too small to be of practical concern;
• not detecting as statistically significantly different a large practical bias between two sites, perhaps because of large variability (poor precision) in the method.

In the language of method qualification or validation, a formal method or technology transfer (TT) process requires a fit-for-purpose design and, consequently, an analysis of the data generated at each site, shaped by the structure of the design, to demonstrate equivalence when equivalence exists. The statistical design and analysis of precision and technology transfer studies are the topics of this series of blogs.

[1] Lung, K. R. Gorko, M. A. Llewelyn, J. and Wiggins, N., Statistical method for the determination of equivalence of automated test procedures. Journal of Automated Methods & Management in Chemistry, 25 (2003), no. 6, pp. 123-127