Article: Strategies to Combat Problems Employing DSDs
Part three of a series of three articles exploring Practical (Real-life) Implementation of Sequential Design of Experiments and the Introduction of Definitive Screening Designs
Written by Dr. Paul Nelson, Technical Director.The criteria often used by experimenters to select and separate a DSD from other classical screening designs (particularly when most if not all the factors are continuous), is their ability to fit unaliased subsets of first and second-order model terms involving no more than three active factors. As demonstrated in my previous article The Evolution of Definitive Screening Designs from Optimal (Custom) DoE, in this case a DSD can potentially provide a shortcut to go directly from screening to finding optimised settings.
Problems however occur if there is no sparsity of effects – if the number of active effects is greater than the number of runs/2 – or there is a great deal of noise in the process or method, or a combination of both. Model selection procedures tend to break down due to the partial aliasing present in DSDs in such cases. The reason for performing a screening design in the first instance is to study many factors of interest, focusing on their main linear effects, in as few experiments as possible. With DSDs you are also given the opportunity to also study curvature in the responses due to the factors under study, but you can be seduced by the opportunity to fit a complete polynomial model for the vital few important factors with a reasonable number of runs. Three strategies to counter the above problems are:
Set aside the factors known to have important effects and initially focus on screening the unknown factors. Including factors known to be important only serves to increase the number of likely active effects and the degree of partial aliasing, as well as the number of runs required, without necessarily adding to your understanding of the true response surface for the critical factors. The vital few unknown factors surviving the initial screen can then be combined with the factors already known to be important and characterised in greater detail during a subsequent optimisation phase of experimentation.
If many terms are likely to appear active, or the noise is expected to be large, or a combination of these, then consider being proactive and supplement your design with more than the required minimum number of runs.
If many terms are active, or the noise is large, or a combination of these, then this is the evidence you need to be reactive and augment your DSD to identify and model more terms (mostly 2nd order).
Proactively Supplementing New DSDs (when in doubt, build it stout):
The addition of Fake factors or columns in your design layout, that you intend to ignore during the analysis, provides a way to increase the number of runs and degrees of freedom when unbiasedly estimating the noise or error variance. Unbiased, because the fake factors are orthogonal to the MLEs of the Real factors, as well as to all the 2nd order effects.
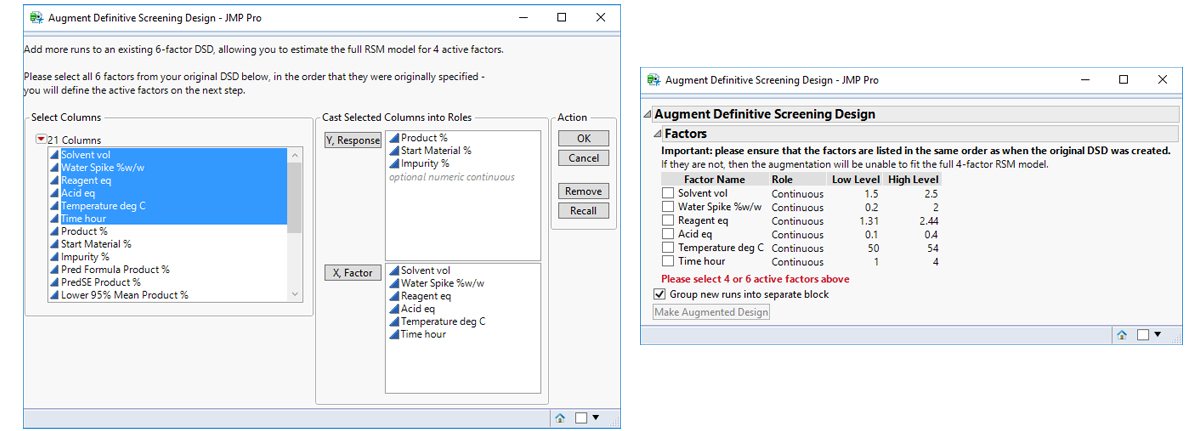
A 17-run DSD, created by the addition of 2 fake factors to the 6-factor Esterification scenario (i.e., 8 rather than 6 factors), is displayed below.
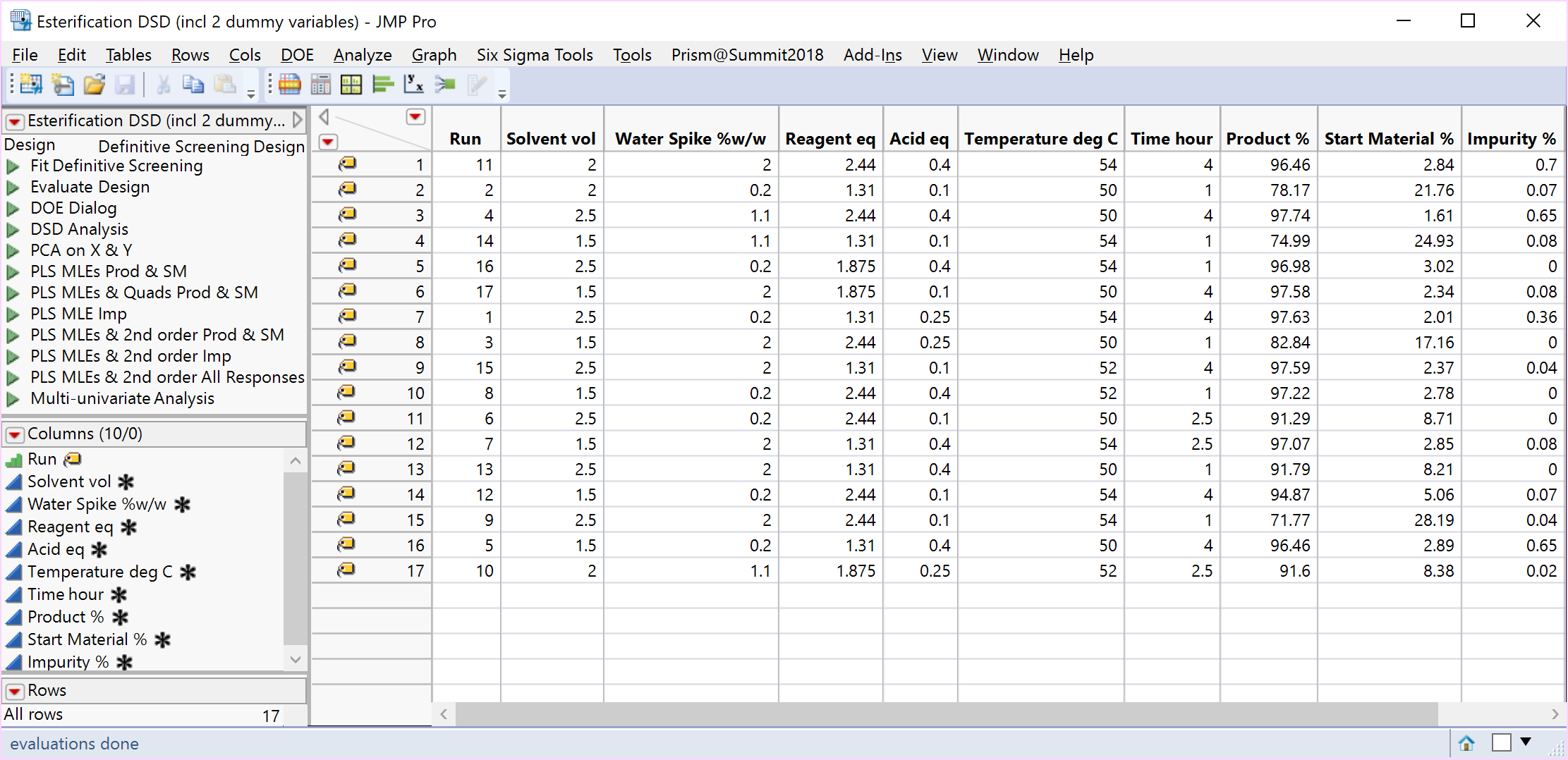
The increase in degrees of freedom can also increase the sensitivity of the tests and consequently a greater number of MLEs and 2nd order terms enter the individual and combined models (left-hand side of the table below). Taking all the (often correlated) responses into account, a multivariate analysis of this data set – which will be covered in a future article – identified just the same three important MLEs as before (Acid, Time and Water Spike) and helped to produce the profiles, which involve 2nd order terms, in the right-hand side of the table below.
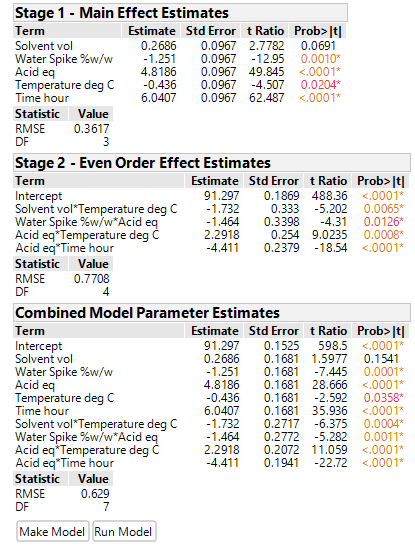
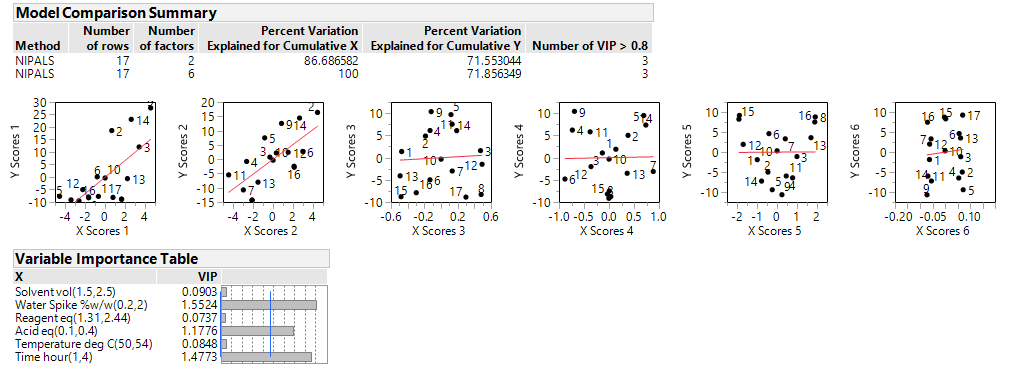
If we increase the noise in the simulated study, then the DSD with the increased number of runs (due to the additional fake factors) should provide better protection against the inflated error variance.
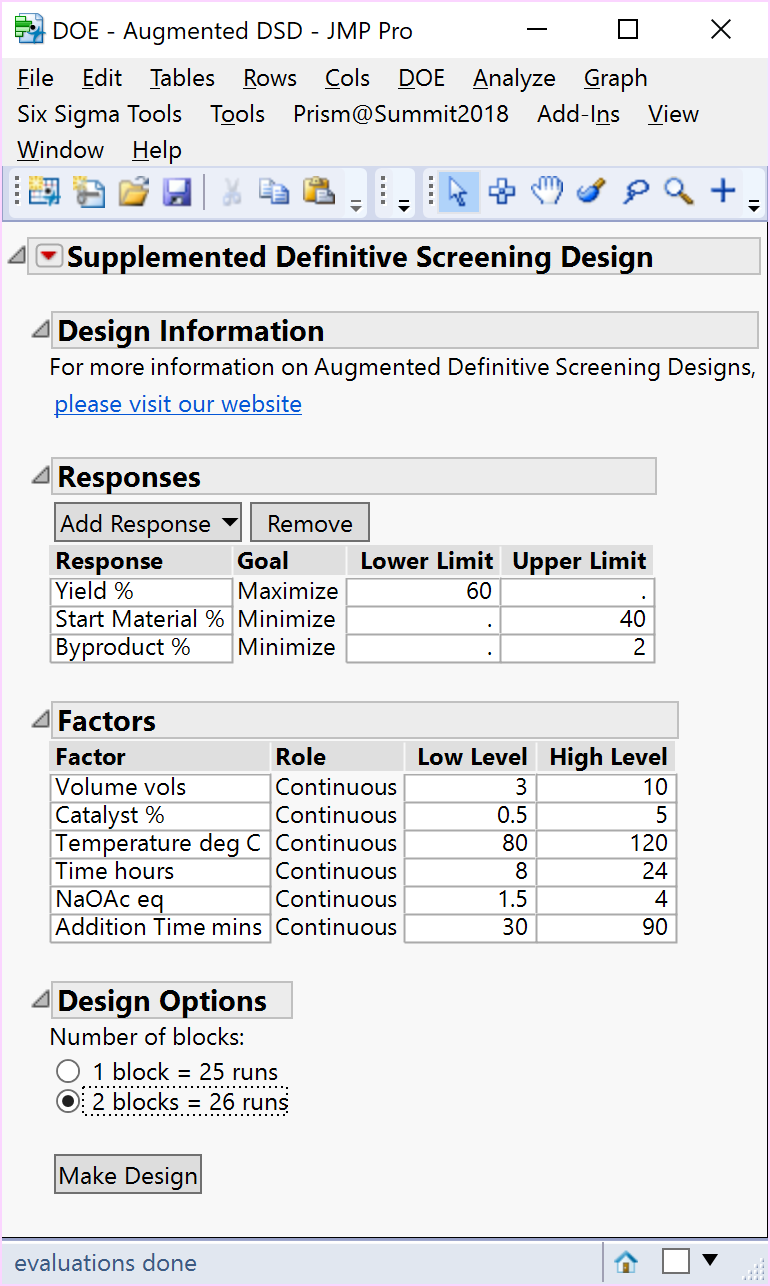
In the other situation, when you suspect more than three active factors and their 2nd order effects are likely to appear, the number of effects is likely to be too great for a full second-order model to be estimated, so what additional runs can be added to the DSD to estimate the complete quadratic model? Optimising a Heck reaction of iodobenzene with cinnamaldehyde, involving DMF solvent volumes, loading of a palladium catalyst, temperature, time, quantity of Sodium Acetate base and addition time, is employed as a second case study from chemical development. This example helps to illustrate how DSDs can be successfully augmented. Previous attempts to improve conversion according to the reported literature had proved “fruitless”.

In this example, the experimenters suspected 4 or more subsets of active factors and 2nd order effects were likely, but for each of three responses, a different number and subset of active factors were possible. The literature on DSDs states you would need to increase the number of factors in the DSD to ≥ 18, for the full RSM model to be estimable for any four factors. One realistic option might be to use a custom D- or Alias-optimal augmentation to search for a supplemented design, to enable you to include all the model terms you want to estimate. But what if you don’t yet know what model you want to estimate and would prefer instead an augmentation that a) provides a wider inductive basis to estimate a range of possible models and b) enables the 1st and 2nd order model terms to continue to be estimated independently and separately?
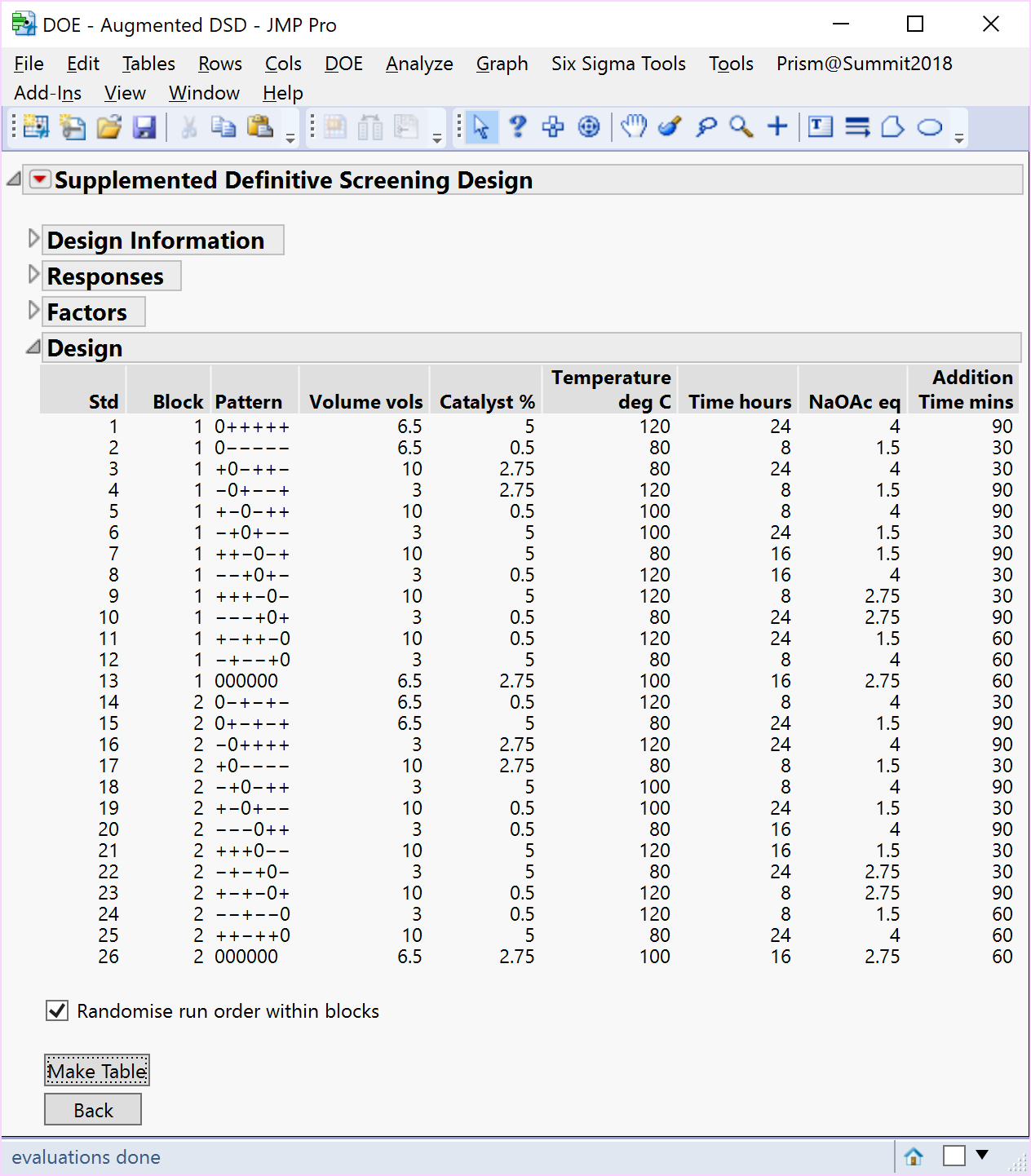
In the case of a 6-factor 13-run DSD Kay (2017) carried out a restricted search for augmentations that preserved the fold-over structure of the design and attempted to retain the orthogonality between 1st and 2nd order effects. These supplemented designs also ensure the design-oriented modelling approach proposed by Jones and Nachtsheim (2017) can continue to be effectively used. Augmentations of the original 13-run design, which enabled fitting the full second-order model for any 4-factor projection, resulted in a randomisation set of twenty 12-run augmentations.
If it is the intention of the experimenter to run the combined 25-run design in one completely randomised block, then randomly select one of the twenty 12-run augmentations, provided by Kay (2017), to supplement the original 13-run DSD and completely randomise the run order.
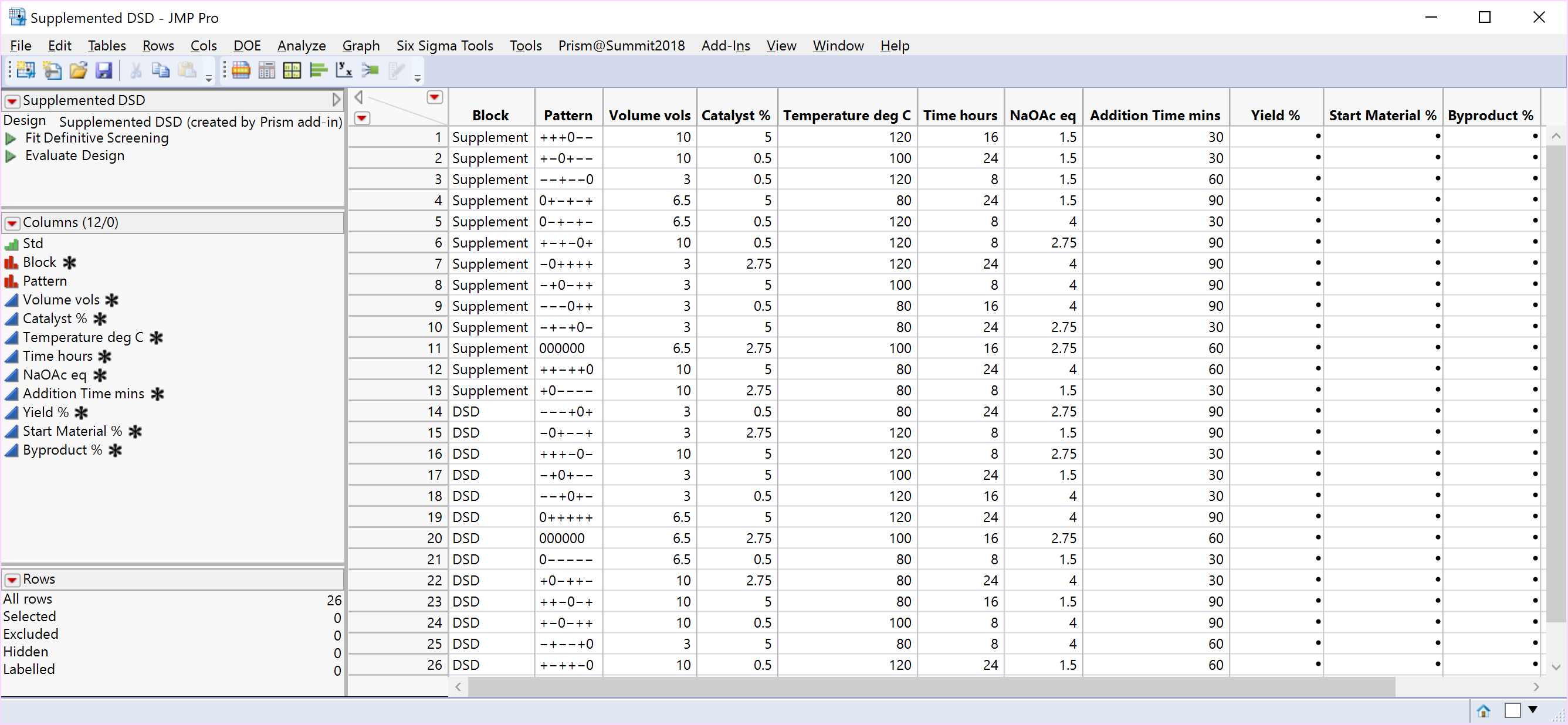
However, if it is the intention of the experimenter to separate and block the original DSD and supplemented parts of the design, then we propose you consider a) including an additional centre point run for the supplemented block of runs to help estimate quadratic terms and b) randomise the order of the blocks, as well as the runs within each block, to ensure the randomisation is valid. A consequence of a) is that the design efficiency is improved along with a significant improvement in the standard errors or precision of your model terms (see the comparison of the combined model parameter estimates for the 25-run and 26-run block augmented experiments below).
Our approach offers both options: a single block of 25 runs, or two blocks each comprising 13 experiments and a valid randomisation scheme in each case. The design-oriented model Fit DSD method proposed by Jones and Nachtsheim (2017) can be applied, whichever design supplement is chosen, and is available as a script that can be run on the data table.
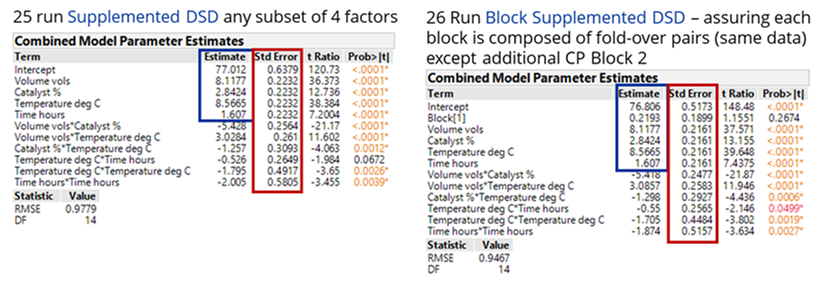
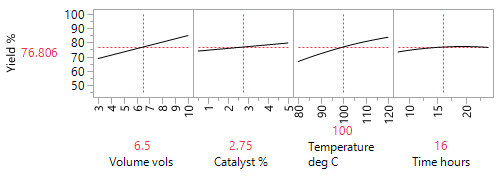
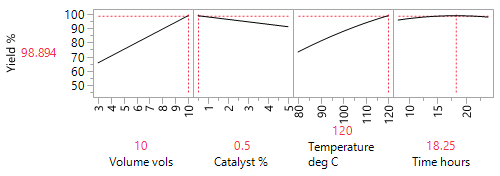
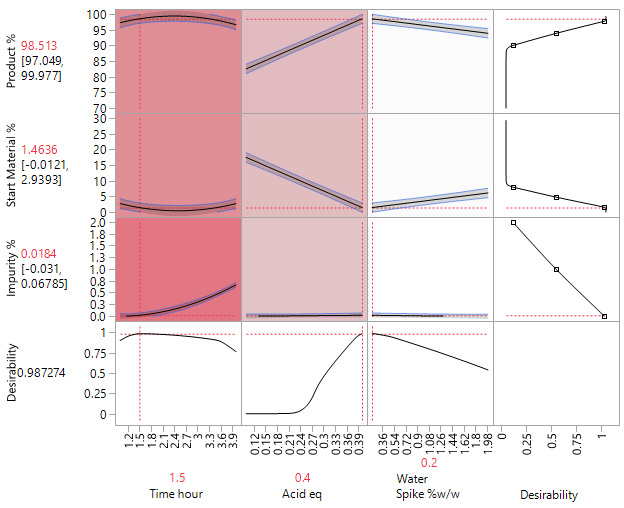
The analysis of this supplemented 26-run blocked DSD, reveals that increased volumes of solvent and temperature, together with a low (0.5%) beneficial loading of the palladium catalyst, counter to what had previously been reported, improved yield from around 60% to 98% (89% isolated).
Finally, if the experimenter desires to restrict the first block of 13 runs to be the original DSD, with the 13-run design supplement forced to be run as a second block, then it is this authors belief that this is an augmentation of an existing DSD; to be run after the original DSD has been performed to enable fitting the second-order model for any 4-factor projection. See the next section.
Reactively Augmenting Existing DSDs:
In the situation where a DSD has already been performed and either a specific subset of 4 active factors, or different subsets of any 4 factors across multiple responses have been identified for further investigation, an augmentation of the existing DSD provides a useful next step for the investigator.
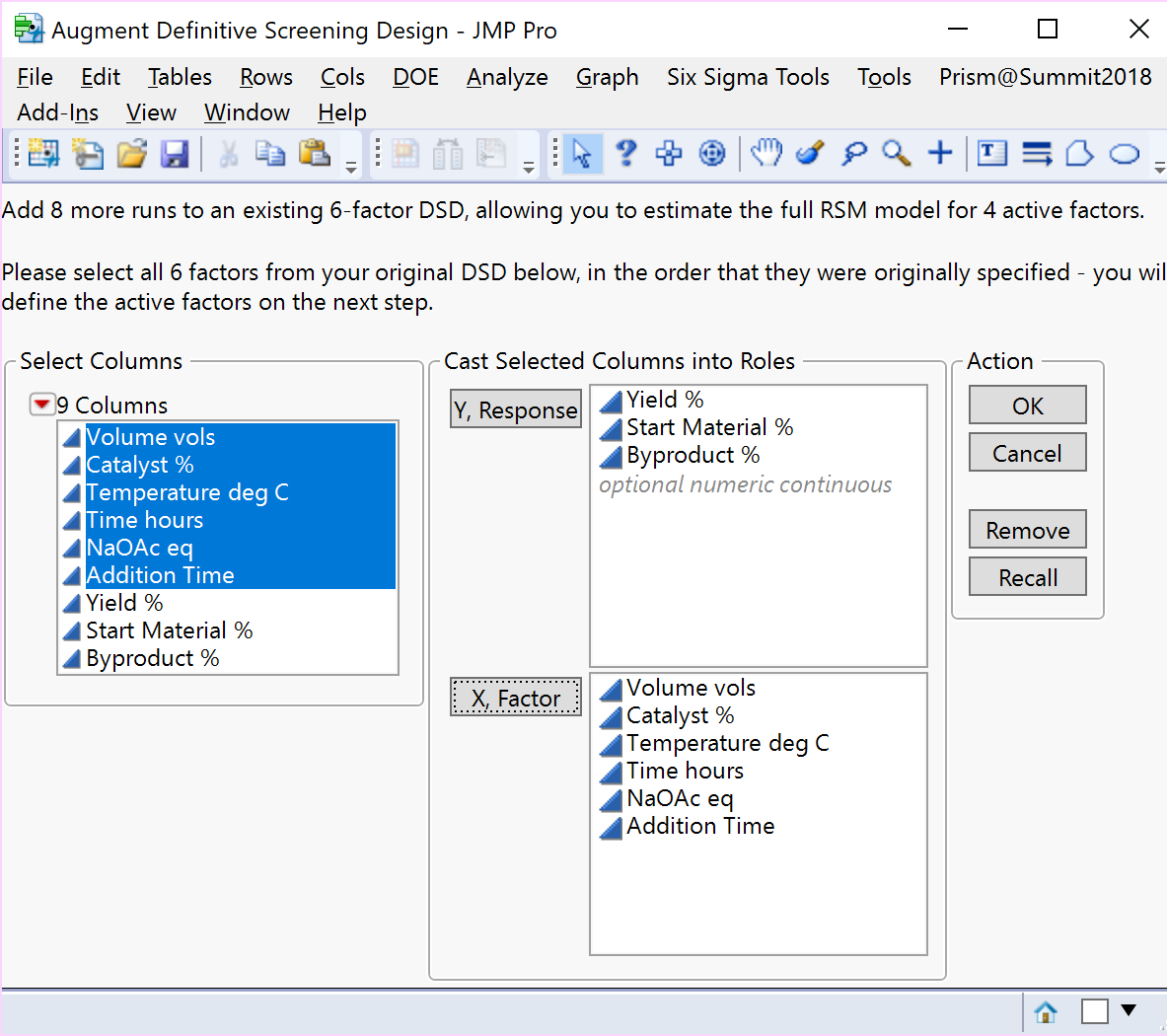
As outlined in the previous section, the randomisation set of twenty 12-run augmentations comprising 6-foldover pairs, with the addition of a centre point run in a second augmented block of experiments, can be used to enable estimation of the full RSM model in the case of an any 4 active factors projection. Typically, you would select all six factors as potentially being active to create a randomly selected second and, by default, randomised block of 13 runs to add to the original DSD.
To estimate the full RSM model for each specific subset of 4 active factors screened from a 6-factor 13-run DSD, Kay (2017) identified two 8-run augmentation sets comprising just 4-foldover pairs with the highest D-efficiency [1]. Based on your choice of which four factors you wish to investigate further, you could randomly select one of the two 8-run augmentations provided by Kay (2017), add a centre point run, and completely randomise the run order in the second augmented block. Choosing the first 4 factors resulted in the 9-run augmentation of the 13-run Heck reaction DSD below.
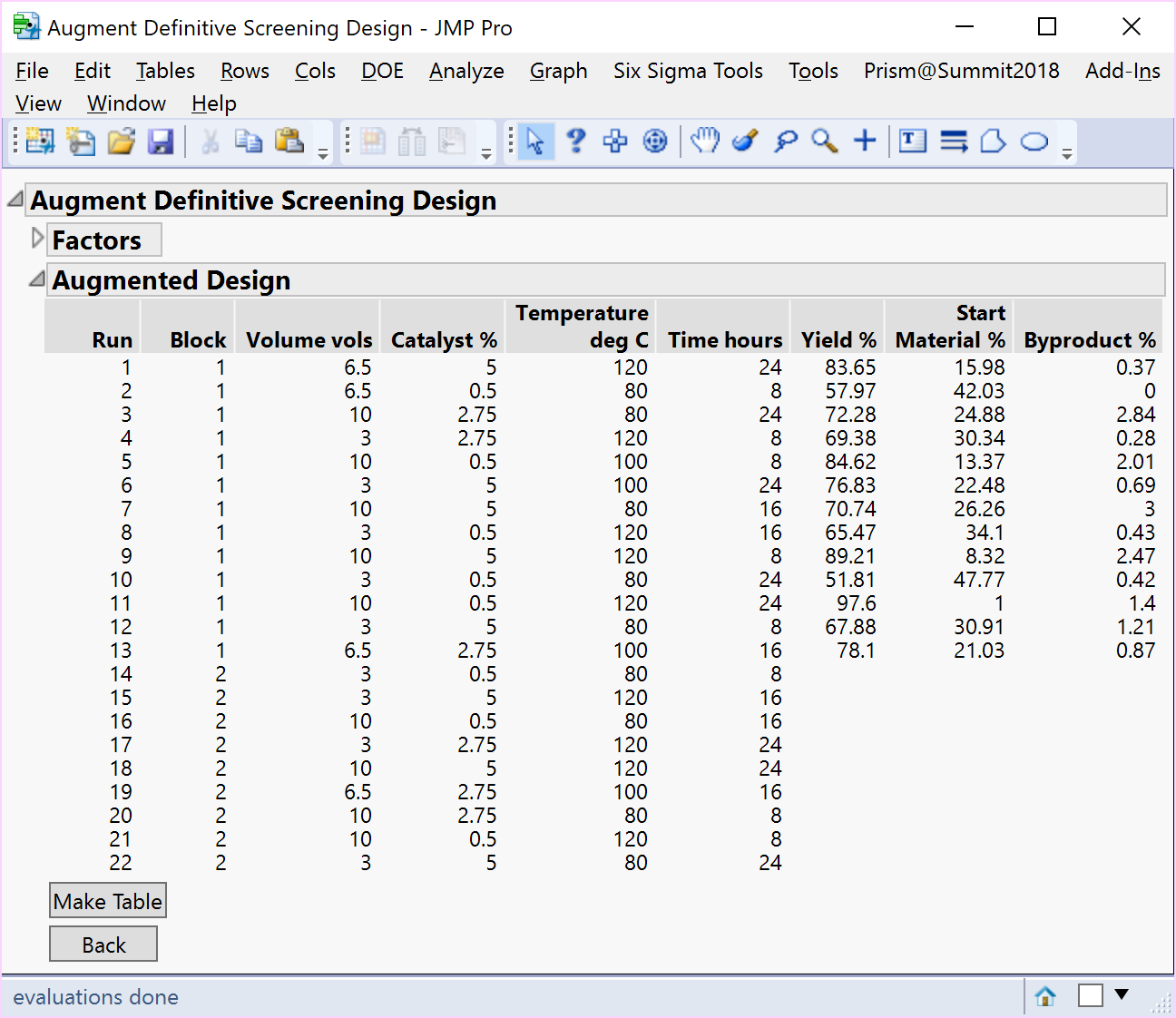
A comparison of the resulting analyses using an 8-run (4-foldover pairs) augmentation without blocks, provided by Kay (2017), with one including blocks, together with the additional centre point, shows that the latter aids the separation, estimation, and improved precision of the quadratic effects of both time and temperature.
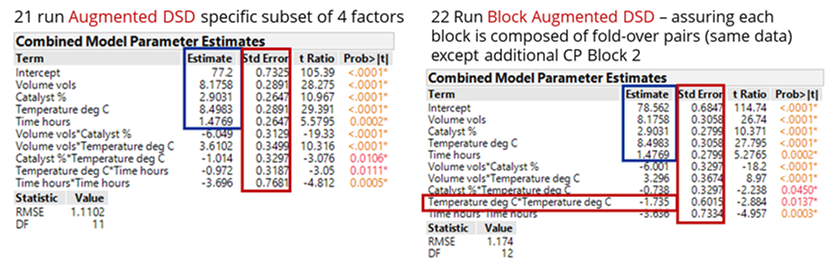
Our practical implementation of the augmentation of fold-over pairs identified by a restricted search algorithm proposed by Kay (2017), suggests that this approach should generalise to DSDs with 7 or more factors, or to the estimation of a full RSM model for any projection of 5 or more factors, or to the accommodation of both.
***
[1] a useful design property.
References
Kay, P. (2017). Augmentations of Definitive Screening Designs to Provide a Simple Workflow for Sequential Experimentation. MSc Thesis
Jones, B., & Nachtsheim, C. (2017). Effective Design-Based Model Selection for Definitive Screening Designs. Technometrics, 59(3), 319-329.
This is the final part of a series of blogs exploring the Practical (Real-life) Implementation of Sequential Design of Experiments and the Introduction of Definitive Screening Designs. The series begins with The Sequential Nature of Classical Design of Experiments, followed by The Evolution of Definitive Screening Designs from Optimal (Custom) Design of Experiments.
For more information about how Prism Training & Consultancy can assist you with statistical support, please contact us to learn more about our services.
Be the first to know about new blogs, upcoming courses, events, news and offers by joining our mailing list here.